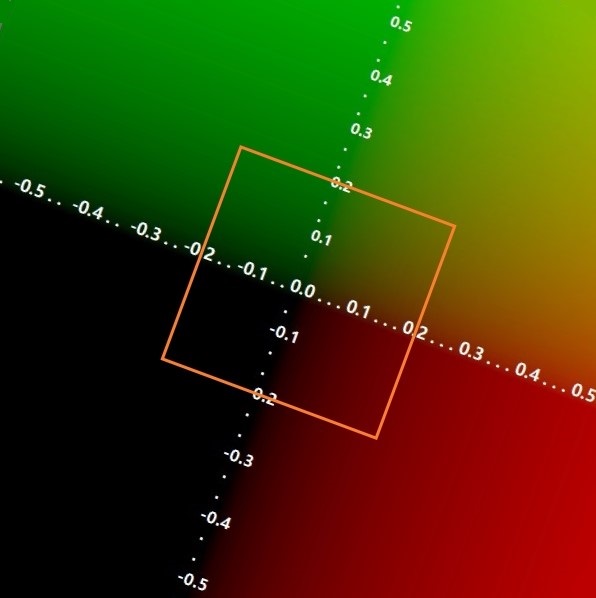
Project Setup
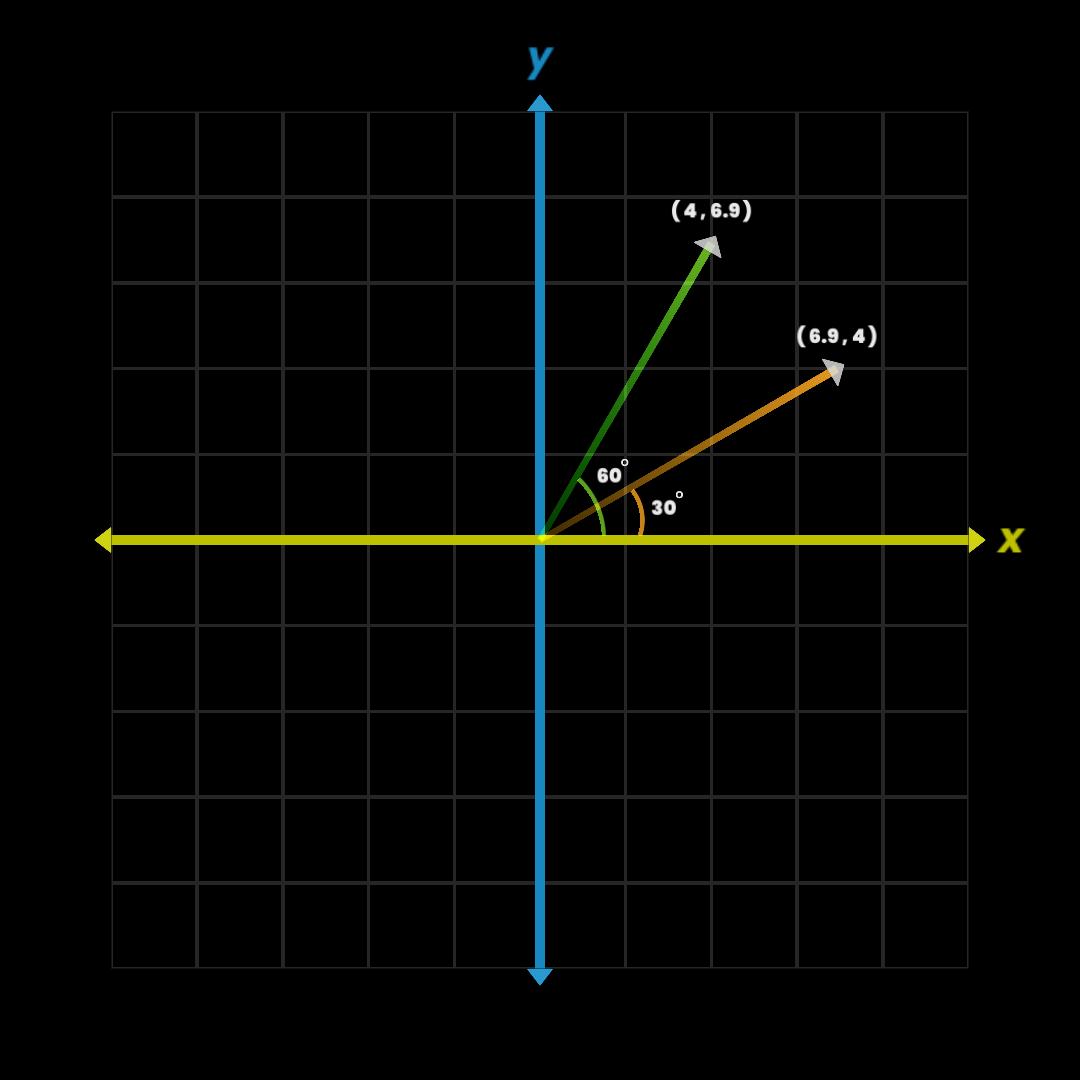
First add a plane then rotate it's face toward camera, or set the plane rotation to (90, 180, 0).
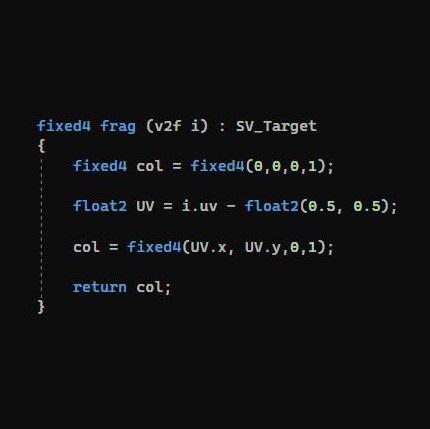
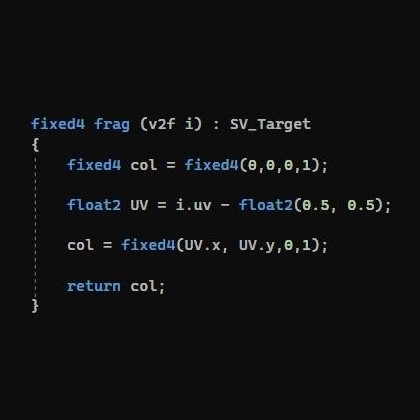
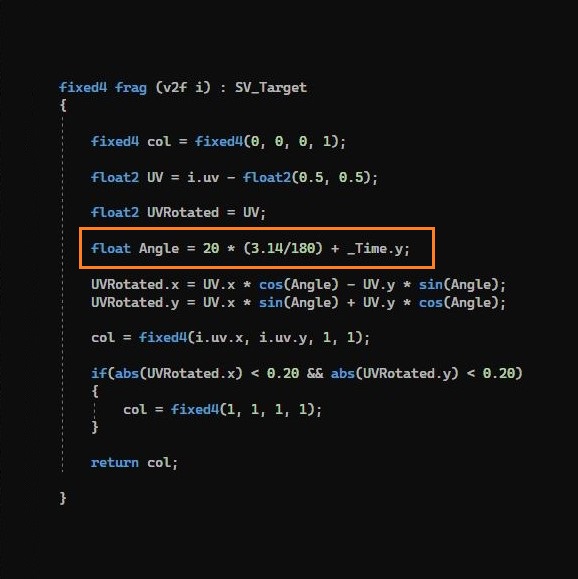
Add a unlit shader and apply it to a material, and apply that material to the plane.
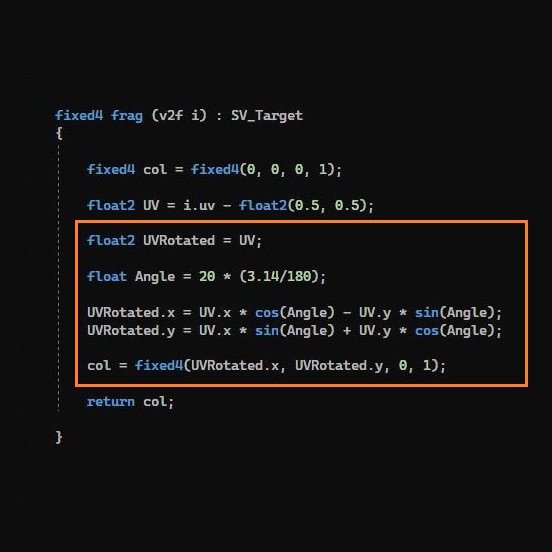
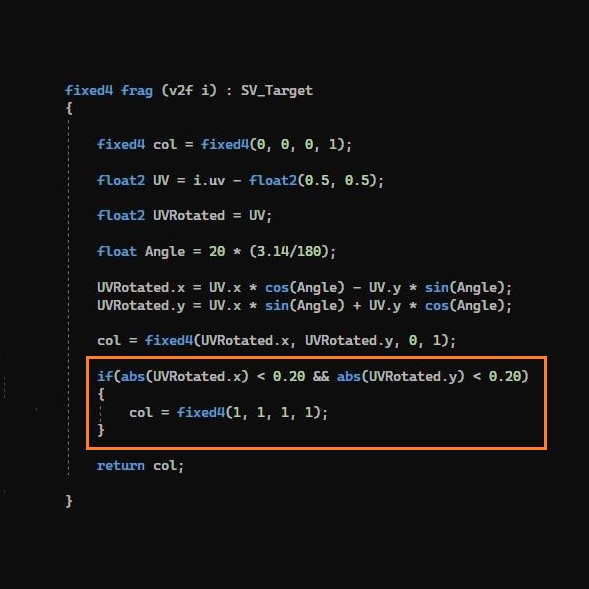
open the Unlit Shader in Visual Studio.
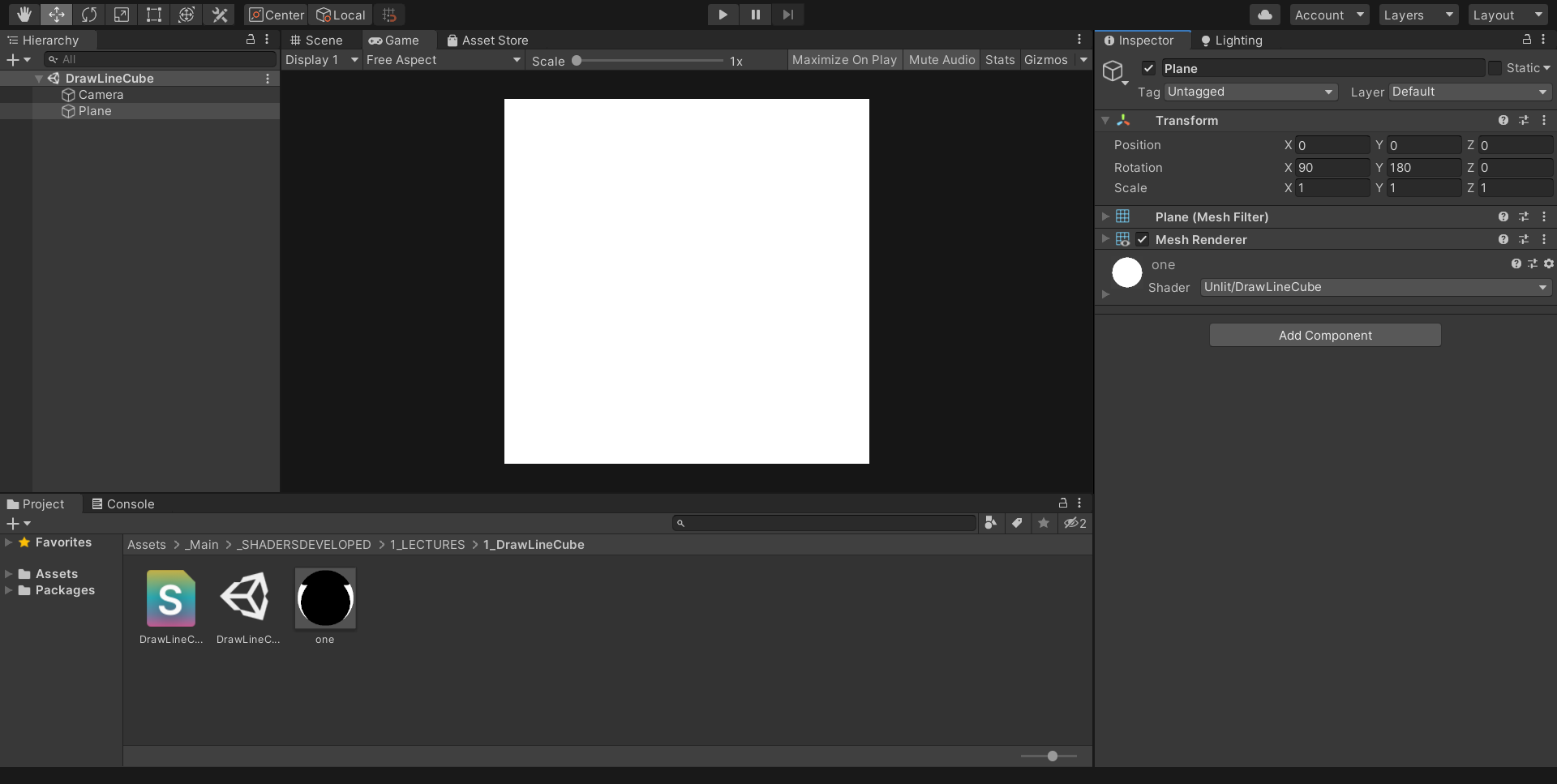
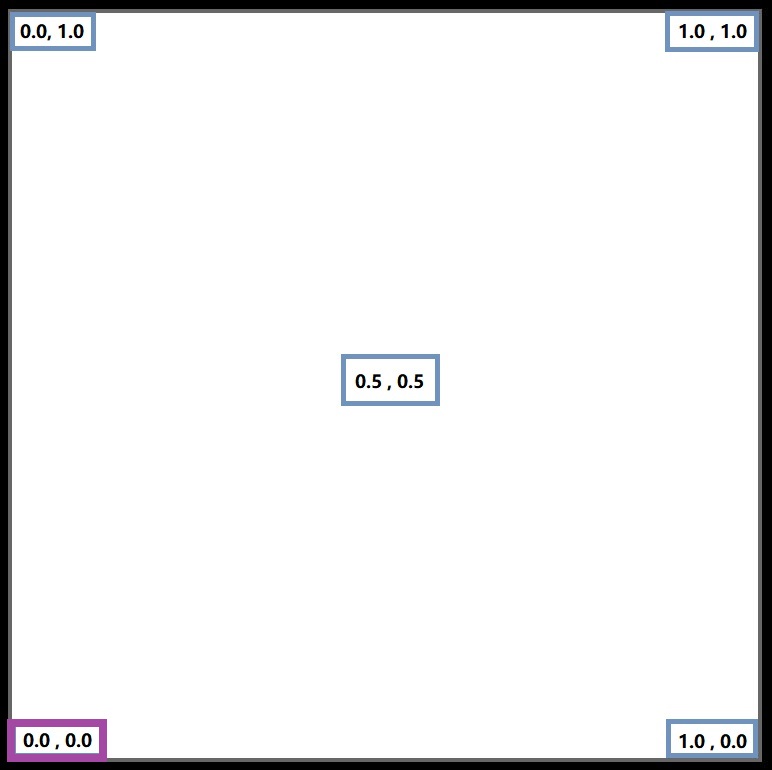
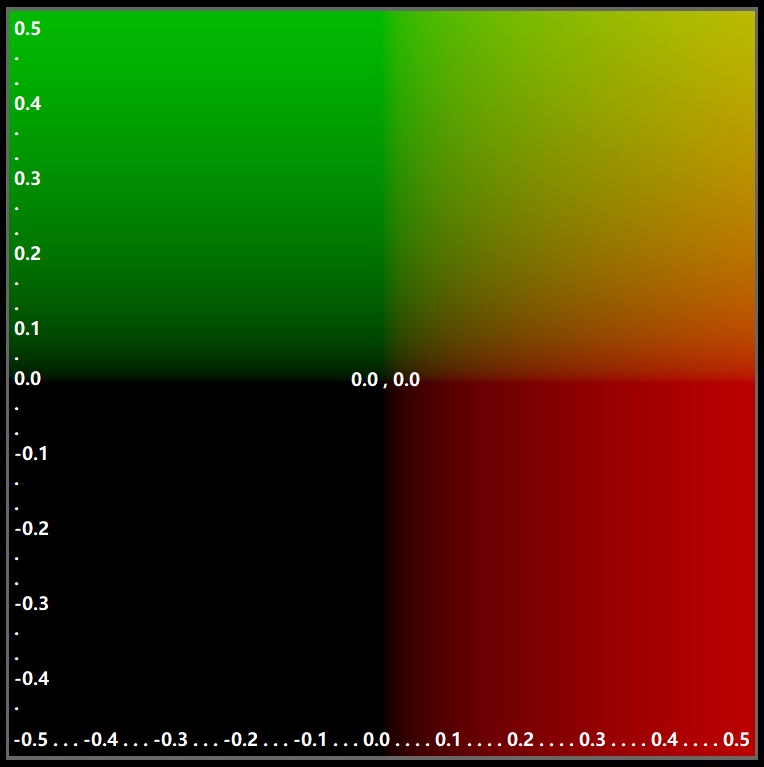
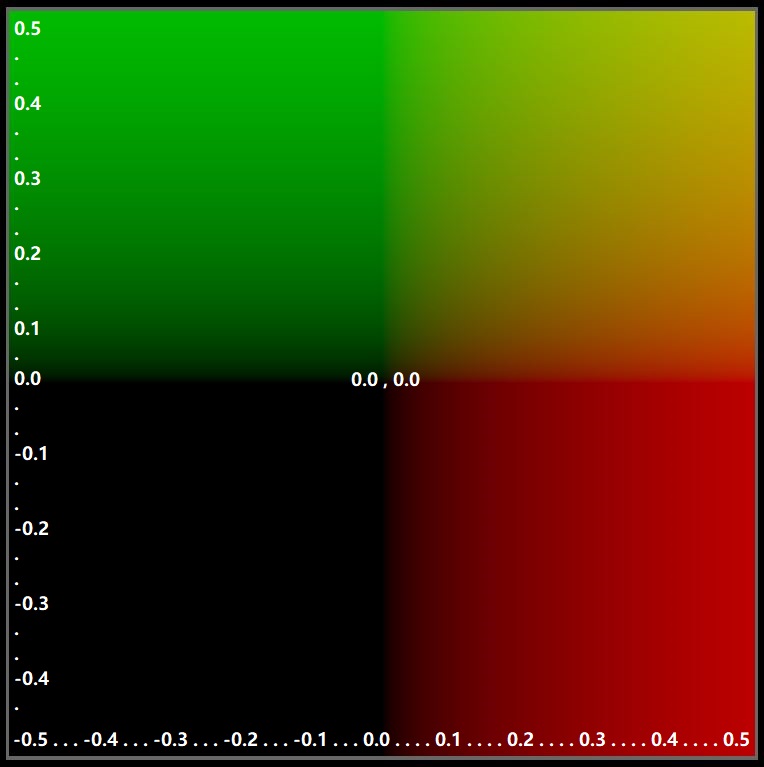
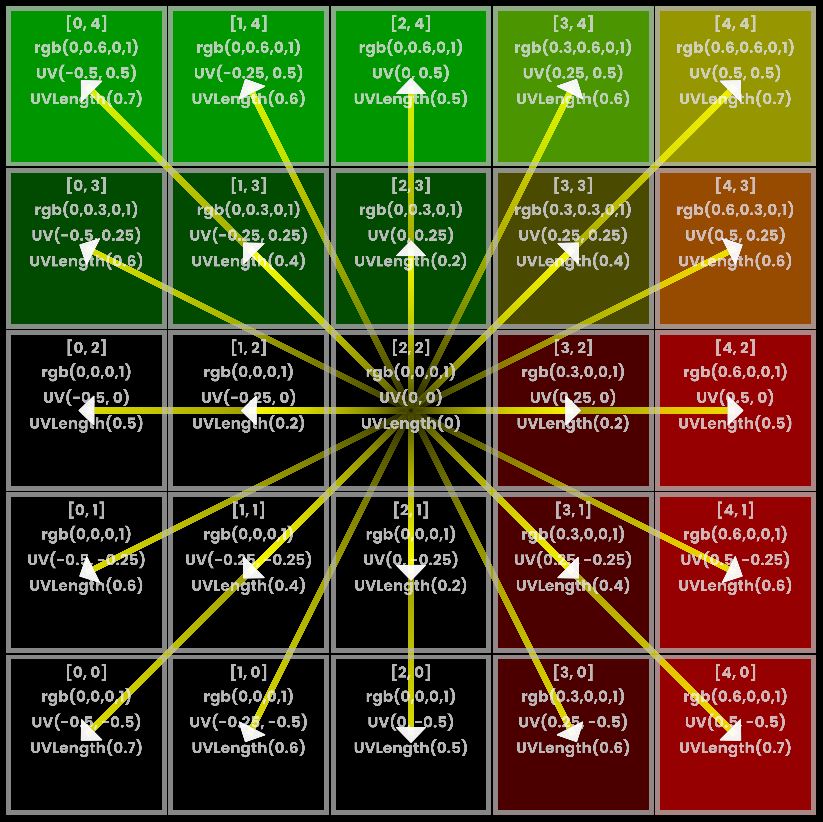
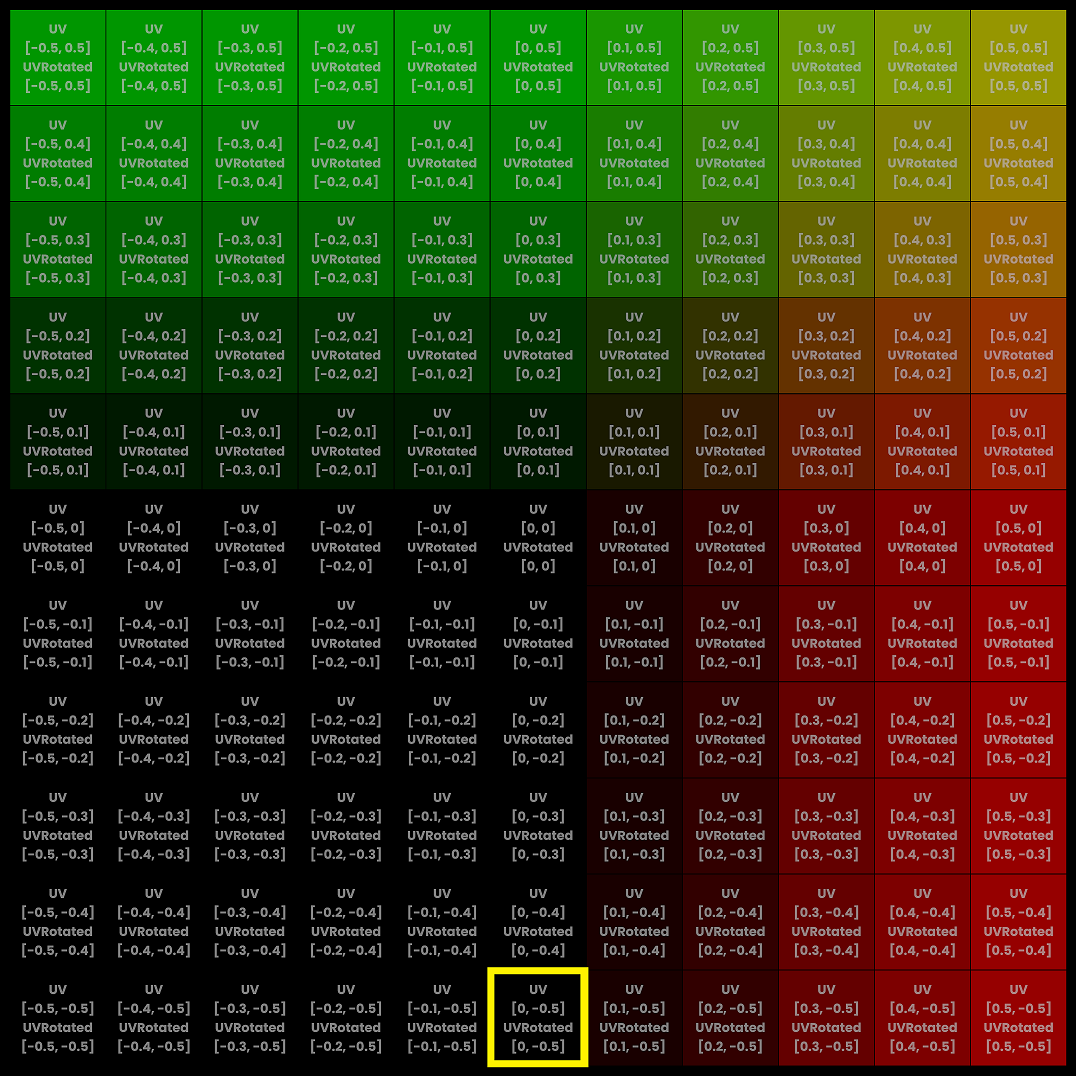
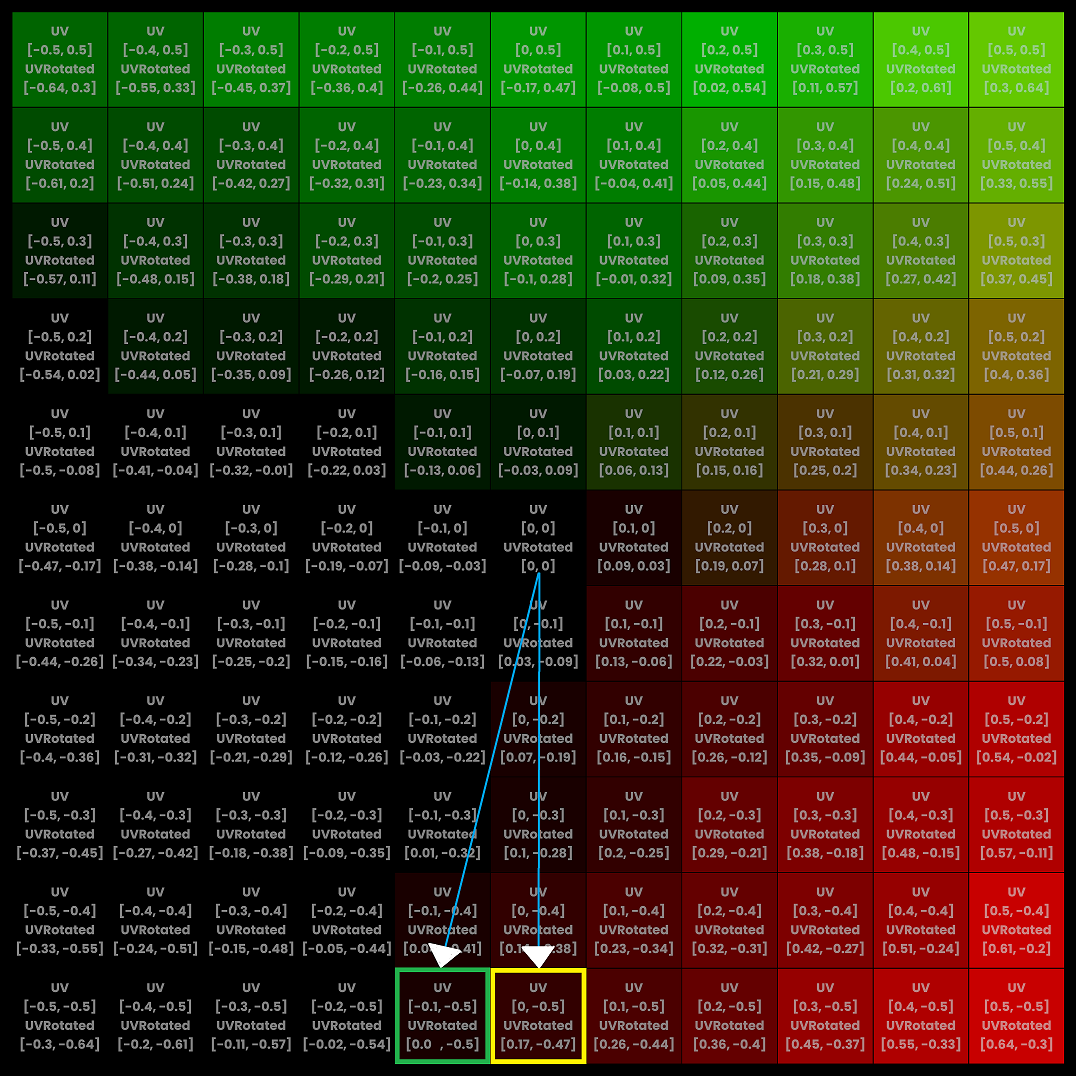
With this rotation of plane, the origin of i.uv is bottom left corner.